外测度并不就是测度。
外测度的定义:

可测的条件:

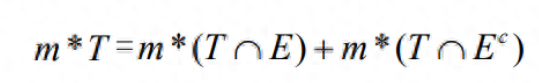
任何一个集合都存在外测度,这是因为集合里面的元素无非是有理数和无理数,而有理数和无理数的测度都可以通过从外部包围的方法计算出它们的外测度。
但一个集合有外测度,并不是就等于这个集合是可测的。集合可测的条件是必须满足可列可加性,也就是不同部分合成的集合的外测度要等于其各部分的外测度之和,就像两本同样大小的书叠放在一起的时候,总的体积等于这两本书的体积之和。
只有当集合的外测度符合可列可加性的时候才是可测的,当集合可测的时候,这个集合的外测度才称为测度。
比如,外测度为0的集合,要通过证明才能确定其是否可测:

另外,A与E的交集加上A与E的补集的交集是A的一个覆盖,由外测度的定义可以得到A的外测度小于等于
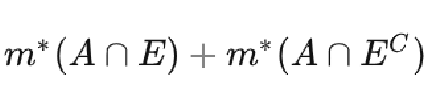
由此得到证明,即A的外测度就等于上式。
只有通过上述证明,这个外测度为0的集合,才能说这个集合的测度是0。
由以上证明也可以看到,零测集都是可测集。