外测度其实就是体积,有如下定理:
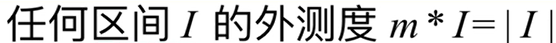

图1
上图中的不等式

图a
是因为I就是包含自身的立方体,按照外测度的定义

,即函数值的下确界要小于等于函数值本身,所以不等式成立。也可以按照
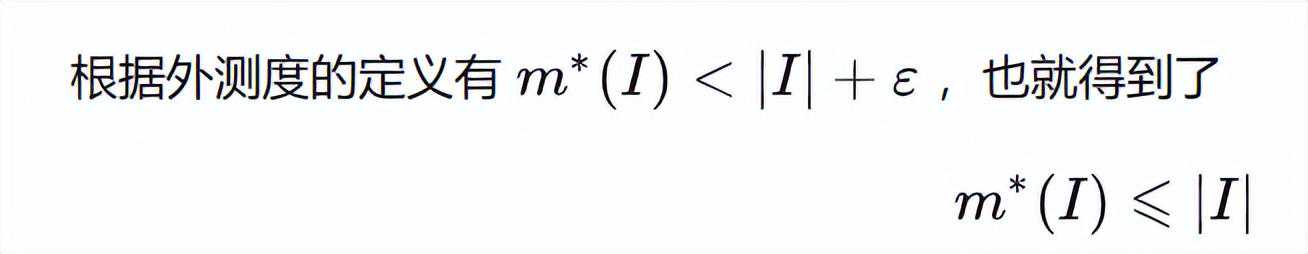
令ε趋于0得到。
再注意图1中的δ是一个无穷小,而δε,所以
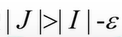
成立。
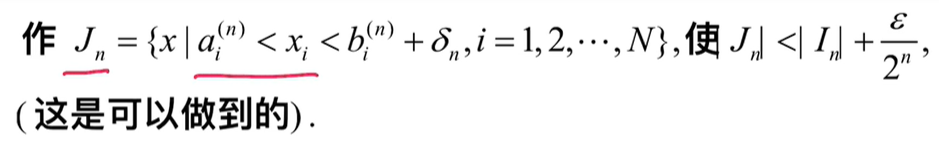

上图中由

图2
推出
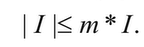
图3
个人是这样理解的:
因为外测度是函数值的下确界,而下确界与函数值只是相差一个无穷小,但图2的不等式两边都是确定的数字,所以两者之间至少相差一个ε,而ε比无穷小大,所以得到图3的结论。
整个证明的思路就是通过中间集合J的创建,想方设法得到图2,然后再得到图3的结论。
最后结合图a和图3,得到要证明的定理。
图1中考虑的是左开右闭区间的情形,其它情况比如左闭右开等等,也可以类似证明。
那么,通过如此复杂的外测度来定义体积,目的是什么呢?
假设区间I全部是有理数组成的集合,由于有理数是可列的,即可以认为有理数之间是隔开来的,这些有理数就不可能填满一条直线、一个平面或者一个长方体,因此就人为地用一个个存在体积的长方体去套这个区间,从而计算出这样的有理数集合的体积。